Penjelasan Kontrol PID Serta Analisis Kesalahan Statis

PID (Proportional-Integral-Derivative) controller adalah sistem kontrol yang menggunakan kombinasi tiga komponen utama: proporsional, integral, dan turunan. Ini membantu dalam menentukan presisi sistem instrumentasi dengan memperhitungkan umpan balik dari sistem tersebut. Pengontrol PID adalah jenis pengontrol konvensional yang sangat umum digunakan di industri saat ini.

Dalam PID controller, tiga komponen utama bekerja bersama-sama untuk menghasilkan sinyal kontrol yang optimal untuk memastikan bahwa proses produksi berjalan dengan baik. Proporsional action memberikan respons yang sebanding dengan besarnya error (perbedaan antara nilai yang diinginkan dan nilai aktual), integral action mengakumulasi error dari waktu ke waktu untuk menanggulangi kesalahan sistematis, dan turunan action merespons laju perubahan error untuk menstabilkan sistem.

Control Valve bertindak sebagai aktuator dalam sistem, mengatur aliran fluida dalam proses industri untuk mencapai level air yang diinginkan, yang disebut Set Point. Error adalah perbedaan antara Set Point dan level air aktual.

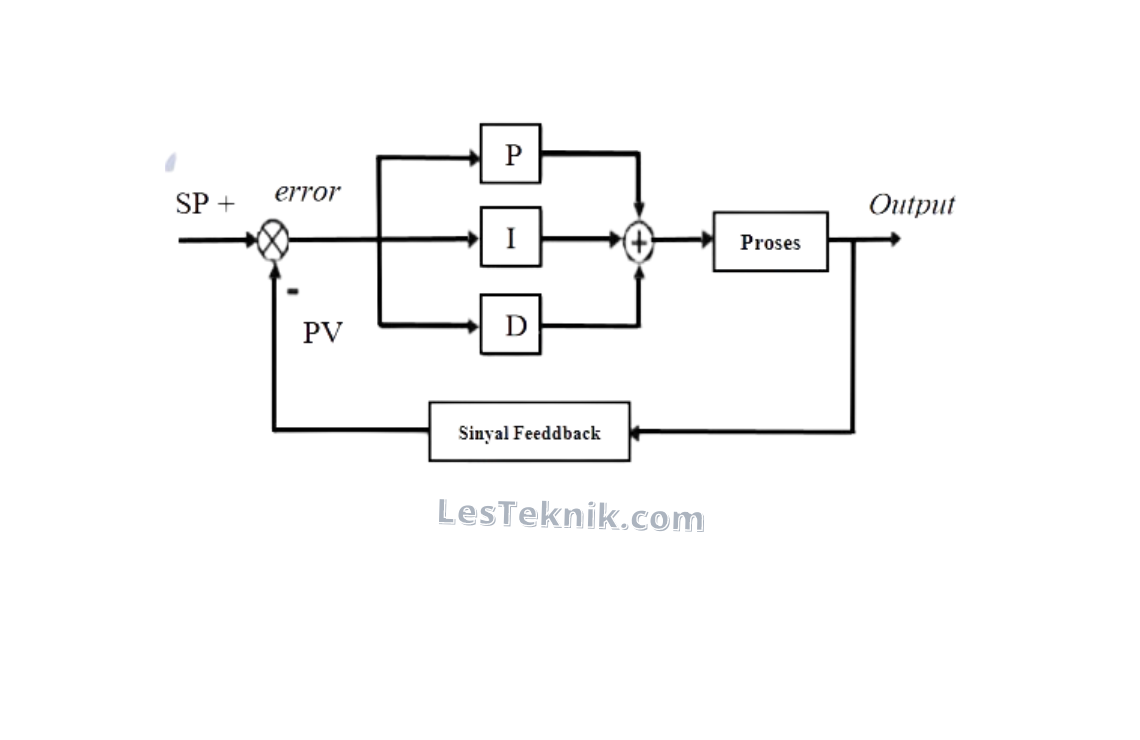
Blok Diagram PID menunjukkan struktur sistem kontrol yang menggunakan PID controller untuk mengatur proses produksi. Ini mencakup semua komponen utama dan bagaimana mereka saling terhubung dan berinteraksi untuk mencapai tujuan kontrol yang diinginkan.

Kontrol PID (Proportional-Integral-Derivative)

PID Blok Diagram dapat dilihat pada gambar dibawah :

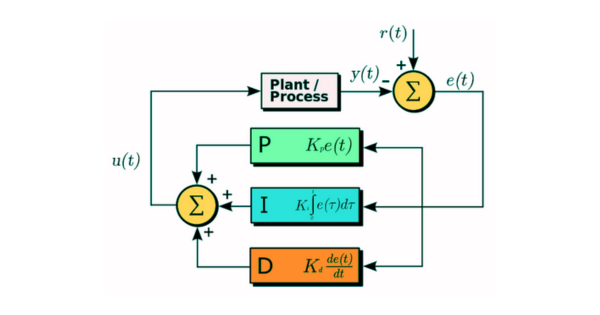
Adapun persamaan Pengontrol PID adalah :

\(m v(t)=K_P\left(e(t)+\frac{1}{T_i} \int_0^t e(t) dt+T_d \frac{d e(t)}{dt}\right)\)

Keterangan :

\(m v(t)=\) output dari pengontrol PID atau Manipulated Variable
\(K p=\) konstanta Proporsional
\(T i=\) konstanta Integral
\(T d=\) konstanta Detivatif
\(e(t)=\) error (selisih antara set point dengan level aktual)

Persamaan Pengontrol PID diatas dapat juga dituliskan sebagai berikut :

\(m v(t)=K_p e(t)+K_i \int_0^t e(t) d t+K_d \frac{d e(t)}{d t}\)

dengan :

\(K_i=K_p \times \frac{1}{T_i} \text { dan } K_d=K_p \times T_d
\)

Ketika kita mengontrol suatu sistem menggunakan pengontrol, penting untuk menetapkan nilai batas minimum dan maksimum untuk variabel yang kita kendalikan (Manipulated Variable). Hal ini membantu memastikan bahwa variabel yang dikendalikan tetap berada dalam rentang yang diinginkan.

Pengontrol PID terdiri dari tiga komponen utama: Proporsional (P), Integral (I), dan Derivatif (D). Ketiga komponen ini dapat digunakan secara terpisah atau kombinasi tergantung pada respons yang diinginkan terhadap sistem yang dikendalikan (plant).

Misalnya, P digunakan untuk menanggapi kesalahan saat ini, I digunakan untuk menanggapi kesalahan masa lalu, dan D digunakan untuk menanggapi perubahan kesalahan di masa depan. Kombinasi dari ketiganya dapat memberikan kontrol yang lebih baik terhadap sistem sesuai dengan kebutuhan spesifik.

1. Kontrol Proporsional (P)

Kontrol Proporsional (P) merupakan salah satu jenis pengontrol yang digunakan dalam sistem kontrol. Pada kontrol P, output pengontrol (u) dihitung dengan mengalikan konstanta proporsional (Kp) dengan nilai kesalahan (e), yang merupakan selisih antara nilai yang diinginkan dan nilai aktual dari variabel yang dikendalikan. Kontrol P memiliki karakteristik yang sederhana dan mudah dipahami, namun memiliki beberapa keterbatasan.

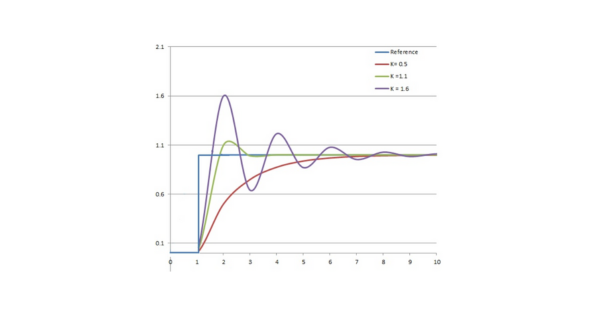
Karakteristik Kontrol Proporsional

Kontrol proporsional menghasilkan output yang sebanding dengan kesalahan yang terjadi. Respons sistemnya dapat disesuaikan dengan mengalikan kesalahan (error) dengan sebuah konstanta Kp, yang dikenal sebagai gain proporsional atau gain kontroler.

Kontrol proporsional dirumuskan:

\( P_{\text {out }}=K_p e(t)\)
\( P_{\text {out }}=K_p\left(Y_{s p}-Y_m\right)\)

Gain yang besar akan menyebabkan perubahan besar pada keluaran untuk nilai kesalahan tertentu. Namun, jika gain terlalu tinggi, sistem akan memerlukan waktu yang lebih lama untuk mencapai kondisi steady-state (seperti yang dijelaskan dalam bagian tuning loop). Sebaliknya, jika gain kecil, respon keluaran juga kecil, mengakibatkan kontroler menjadi kurang responsif atau sensitif. Akibatnya, respon kontroler terhadap gangguan akan lebih lambat.

Ciri-ciri dari pengontrol proporsional antara lain:

• Koreksi Kesalahan Proporsional: Output dari pengontrol proporsional berbanding lurus dengan besarnya kesalahan antara nilai yang diinginkan dan nilai aktual variabel yang dikendalikan. Artinya, semakin besar selisih antara nilai yang diinginkan dan aktual, semakin besar pula output kontrolnya.
• Pengaruh Kp pada Respons Sistem: Nilai Kp menentukan seberapa cepat sistem bereaksi terhadap kesalahan. Jika nilai Kp kecil, respons sistem akan lambat, yang menyebabkan penambahan waktu naik (rise time). Namun, jika nilai Kp ditingkatkan, sistem akan merespons lebih cepat dan waktu naik akan berkurang.
• Kestabilan Sistem: Meskipun peningkatan nilai Kp dapat meningkatkan respons sistem, jika nilai Kp terlalu besar, sistem bisa menjadi tidak stabil atau mengalami osilasi. Ini bisa terjadi karena sistem berusaha terlalu keras untuk mengejar nilai yang diinginkan, tanpa memperhitungkan efek dari faktor lain seperti inertia atau delay.
• Steady State Error: Meskipun kontrol P dapat membantu mengurangi kesalahan steady state (perbedaan antara nilai yang diinginkan dan nilai aktual saat mencapai keseimbangan), biasanya tidak dapat menghilangkannya sepenuhnya.

Dengan memperhatikan karakteristik dan keterbatasan ini, penggunaan kontrol proporsional seringkali sesuai untuk aplikasi yang relatif sederhana dan membutuhkan respons yang cepat terhadap perubahan. Namun, untuk sistem yang lebih kompleks, kombinasi dengan komponen kontrol lain seperti Integral (I) dan Derivatif (D) sering diperlukan untuk mencapai performa yang optimal.

2. Kontrol Integral (I)

Kontrol Integral (I) adalah salah satu komponen penting dalam sistem kontrol yang bertujuan untuk menghasilkan respons sistem dengan kesalahan steady state yang nol. Komponen ini memperhitungkan integral dari kesalahan (error) dari waktu awal hingga waktu saat ini, yang memungkinkan sistem untuk menyesuaikan keluarannya sehingga mencapai nilai yang diinginkan tanpa adanya kesalahan steady state.

 

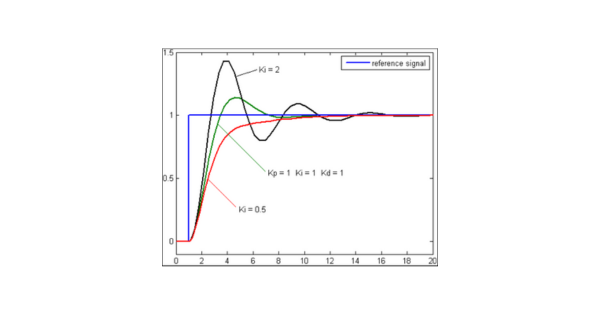
Karakteristik Kontrol Integral

Peranan integral berkaitan dengan ukuran dan durasi kesalahan. Dalam kontroler PID, integral merupakan total kesalahan dari waktu ke waktu dan menyimpan koreksi sebelumnya terhadap offset. Setiap kesalahan yang terakumulasi dikalikan dengan gain integral (Ki) untuk menghasilkan output kontroler.

Kontrol Integral dirumuskan dengan:

\(I_{\text {out }}=K_i \int_0^t e(\tau) d \tau\)

Integral berperan dalam mempercepat pencapaian setpoint dan menghilangkan kesalahan steady-state yang mungkin muncul pada kontroler proporsional. Namun, karena integral bereaksi terhadap kesalahan yang terakumulasi dari sebelumnya, hal ini dapat menyebabkan overshoot.

Beberapa poin penting tentang kontrol integral:

• Peran Integrator dalam Menghilangkan Kesalahan Steady State: Tanpa komponen integrator, pengontrol proporsional tidak dapat menjamin kesalahan steady state yang nol. Integrator mengakumulasi kesalahan dari waktu ke waktu dan bertindak untuk menghilangkan selisih antara nilai yang diinginkan dan nilai aktual.
• Perhitungan Output Integrator: Output dari pengontrol integral dihitung dengan mengintegrasikan kesalahan terhadap waktu dan mengalikannya dengan konstanta integral (Ki). Rumus umumnya adalah \(u(t) = ∫e(t)dt * Ki\). Di sini, Ki adalah konstanta integral yang memengaruhi seberapa cepat sistem bereaksi terhadap kesalahan.
• Pengaruh Konstanta Integral Ki: Nilai Ki yang terlalu tinggi dapat menyebabkan respon sistem menjadi tidak stabil, bahkan menyebabkan osilasi. Namun, nilai Ki yang tepat dapat memperbaiki respons sistem dan menghilangkan kesalahan steady state dengan cepat.
• Respons Lambat: Salah satu keterbatasan kontrol integral adalah respons yang lambat karena mengakumulasi kesalahan dari waktu ke waktu. Hal ini bisa menyebabkan penundaan dalam mencapai nilai yang diinginkan.
• Keluaran Pengontrol sebagai Luas Bidang Kesalahan: Output dari pengontrol integral merupakan luas bidang yang dibentuk oleh kurva kesalahan terhadap waktu. Semakin besar luas bidang ini, semakin besar koreksi yang dibuat oleh pengontrol integral.

Kontrol integral merupakan komponen yang penting untuk menghasilkan respons sistem yang stabil dan bebas dari kesalahan steady state. Namun, penggunaannya perlu dipertimbangkan dengan cermat untuk menghindari efek samping seperti respons yang lambat atau bahkan ketidakstabilan sistem.

3. Kontrol Derivatif (D)

Kontrol Derivatif (D) merupakan komponen penting dalam sistem kontrol yang menanggapi laju perubahan kesalahan (error) terhadap waktu. Output dari kontrol derivatif memiliki sifat yang mirip dengan operasi diferensial, di mana perubahan mendadak pada masukan akan menghasilkan perubahan yang cepat dan besar pada output. Namun, kontrol derivatif tidak akan menghasilkan output jika tidak ada perubahan pada masukan (error).

 

Karakteristik Kontrol Derivatif

Untuk menghitung kesalahan pada proses, kita menilai kemiringan kesalahan pada setiap saat dan mengalikan perubahan tersebut dengan gain derivatif Kd.

Kontrol derivatif dirumuskan dengan:

\(D_{\text {out }}=K_d \frac{d e(t)}{d t}\)

Beberapa poin penting tentang kontrol derivatif:

• Respons terhadap Perubahan Kesalahan: Kontrol derivatif bereaksi terhadap laju perubahan kesalahan terhadap waktu. Ini berarti bahwa jika terjadi perubahan tiba-tiba dalam kesalahan, output dari kontrol derivatif akan menghasilkan respons yang cepat dan besar.
• Formula Output Kontrol Derivatif: Output dari kontrol derivatif dihitung sebagai \(G(s) = s * Kd\), di mana s adalah variabel kompleks yang merepresentasikan laju perubahan, dan Kd adalah konstanta derivatif. Dengan ini, kontrol derivatif dapat mengantisipasi perubahan dalam kesalahan dan memberikan koreksi sebelum kesalahan menjadi besar.
• Koreksi Awal: Salah satu karakteristik unik dari kontrol derivatif adalah kemampuannya untuk mendahului kesalahan dengan memberikan koreksi awal. Ini membantu meningkatkan stabilitas sistem dengan mengurangi overshoot dan meningkatkan respons sistem pada periode peralihan.
• Penggunaan Bersama Komponen Lain: Kontrol derivatif umumnya tidak digunakan sendiri tanpa adanya komponen kontrol lainnya seperti proporsional dan integral. Ini karena kontrol derivatif lebih efektif pada periode peralihan dan tidak memperkecil kesalahan steady state.
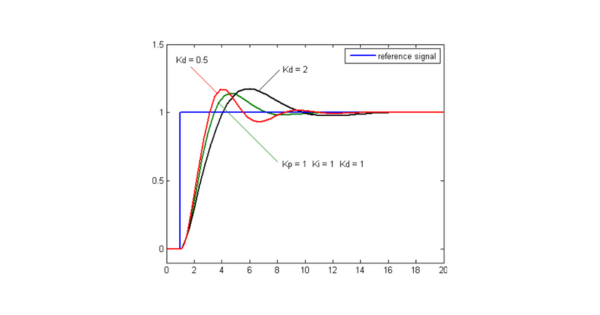
• Peningkatan Stabilitas: Dengan meningkatkan nilai konstanta derivatif Kd, stabilitas sistem dapat ditingkatkan dan overshoot dapat dikurangi. Namun, nilai Kd yang terlalu besar dapat menyebabkan sistem menjadi tidak stabil.

Kontrol derivatif digunakan terutama untuk mempercepat respons awal sistem dan mengantisipasi perubahan dalam kesalahan. Namun, penggunaannya perlu dipertimbangkan dengan hati-hati dan seringkali digunakan bersama dengan komponen kontrol lainnya untuk mencapai kinerja sistem yang optimal.

Tunning nilai Kp, Ki dan Kd

Untuk menentukan nilai Kp, Ki, dan Kd, ada beberapa pendekatan yang dapat dilakukan, salah satunya adalah dengan melakukan penyetelan satu per satu. Langkah pertama adalah menyetel nilai Kp (Gain proporsional), dimulai dengan mencari respons sistem yang paling cepat dengan meminimalkan waktu naik.

Penting untuk tidak memberikan nilai Kp yang terlalu besar atau terlalu kecil untuk menghindari masalah. Setelah respons dianggap cukup optimal, langkah selanjutnya adalah menetapkan nilai Kd (Gain Derivatif) untuk meredam atau bahkan menghilangkan osilasi dengan mengecilkan amplitudo.

Langkah terakhir dalam menyetel nilai Gain adalah menentukan nilai Ki (Gain Integral). Penyetelan Ki diperlukan jika sistem mengalami kesalahan steady state, yang terjadi ketika ada perbedaan antara nilai setpoint dan nilai sistem saat mencapai kondisi steady state.

Kesalahan Statis dalam Kontrol PID

Kesalahan statis dalam kontrol PID mengacu pada kesalahan yang tetap atau tidak berubah antara nilai yang diinginkan (setpoint) dan nilai yang dicapai oleh sistem setelah mencapai kondisi tunak (steady-state).

Dalam sistem kontrol, tujuan utama dari PID adalah untuk meminimalkan kesalahan antara setpoint dan output sistem. Namun, dalam beberapa kasus, kesalahan statis dapat terjadi meskipun kontrol PID telah diimplementasikan.

Penyebab Kesalahan Statis

Beberapa faktor yang dapat menyebabkan kesalahan statis dalam sistem kontrol PID antara lain:

• Kesalahan dalam Model Sistem: Jika model matematis sistem tidak akurat atau tidak lengkap, hal ini dapat menyebabkan kesalahan dalam perhitungan kontrol PID dan akhirnya menghasilkan kesalahan statis.
• Gangguan Eksternal: Gangguan eksternal seperti perubahan beban atau gangguan lingkungan dapat menyebabkan sistem tidak mencapai nilai setpoint yang diinginkan.
• Kelebihan Pemrosesan: Pemilihan parameter PID yang tidak tepat atau pengaturan yang terlalu agresif dapat menyebabkan osilasi dan kesalahan statis dalam sistem.

Dampak Kesalahan Statis

Kesalahan statis dalam sistem kontrol PID dapat memiliki dampak yang signifikan, termasuk:

• Kinerja yang Tidak Optimal: Kesalahan statis dapat mengakibatkan sistem tidak mencapai nilai setpoint yang diinginkan, yang pada gilirannya dapat mengurangi kinerja keseluruhan sistem.
• Ketidakstabilan Sistem: Jika kesalahan statis tidak ditangani dengan benar, hal ini dapat menyebabkan sistem menjadi tidak stabil dan menghasilkan osilasi atau bahkan kegagalan sistem.
• Kerusakan Peralatan: Kesalahan statis yang signifikan dapat menyebabkan komponen sistem mengalami kelelahan atau kerusakan lebih awal dari yang diharapkan.

Teknik-Teknik Pengurangan Kesalahan Statis

Untuk mengatasi masalah kesalahan statis dalam kontrol PID, beberapa teknik yang umum digunakan antara lain:

• Penyetelan Parameter PID: Menyesuaikan parameter proporsional, integral, dan derivatif PID untuk mencapai respons yang diinginkan dari sistem.
• Feedforward Control: Menambahkan kontrol feedforward untuk mengkompensasi gangguan eksternal dan meningkatkan respons sistem terhadap perubahan setpoint.
• Integrator Windup Protection: Mengimplementasikan perlindungan terhadap integrator windup, yang dapat terjadi ketika nilai output sistem terlalu jauh dari setpoint yang diinginkan.
• Penggunaan Sensor dan Aktuator yang Lebih Akurat: Menggunakan sensor dan aktuator yang lebih akurat dan responsif untuk mengurangi kesalahan dalam pengukuran dan aksi kontrol.

Kesimpulan

Kesalahan statis dalam kontrol PID adalah masalah yang umum terjadi dalam desain dan implementasi sistem kontrol. Memahami penyebab dan dampak kesalahan statis, serta menggunakan teknik-teknik yang tepat untuk menguranginya, sangat penting untuk mencapai kinerja yang optimal dari sistem kontrol PID.

Dengan menggunakan pendekatan yang tepat, kesalahan statis dapat diminimalkan atau bahkan dihilangkan sepenuhnya, sehingga meningkatkan efisiensi dan keandalan sistem kontrol.